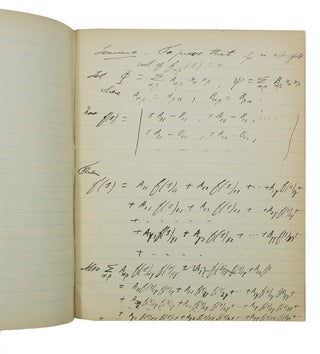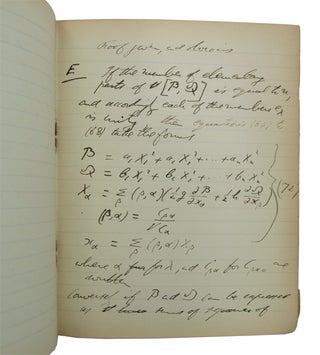Mathematical Manuscript Notebooks.
1900.
The Only Known Mathematical Manuscript of Alfred North Whitehead
[Whitehead, Alfred North]. Mathmatical Manuscript Notebooks. Whitehead (1861-1947) Writing in manuscript. [Unsigned and undated, circa: 1900].
Two composition notebooks. Quarto (202 x 160 mm). 50 ff each, written primarily on rectos in black ink, with a few notes on versos, each page with approx. 15-20 lines of manuscript. Ruled paper self-wrappers, first and last leaves toned and worn, some chipping to edges, corners worn, lower right corner of last 2 ff in vol.I missing with some loss to text. Fragile.
Two sequential notebooks, divided into three sections as follows:
Part 1: 21 pp, on ff 1r-20r of first notebook. In black ink, written on versos. Treating Karl Weierstrass’s 1858 “Über ein die homogenen Functionen zweiter Grades betreffen des Theorem.”
Part 2: 64 pp, on ff 24r-50r of first notebook, and 1r-32r of second notebook. Treating Karl Weierstrass’s 1868 “Zu theorie der bilinearen und quadratischen Formen.”
Part 3: 15 pp, on ff 34r-47r of second notebook. Treating Fredinand Georg Frobenius’ proof of Karl Weierstrass’ theorem.
WITH: WHITEHEAD, J[essie) M[arie). Autograph notebook signed, ("J.M. Whitehead"), 60 pp. Cloth-backed flexible boards. Being class notes for librarian/archivist school, majority written in short-hand. The three housed together in a full calf clamshell.
The only known surviving mathematical manuscript by Alfred North Whitehead. Manuscript material by Whitehead has never come to public auction, and in fact, any manuscript material by him is of the utmost rarity, with even institutional holdings being very minimal.
It is common academic tradition to leave one's Nachlass to a favored graduate student or in a scholarly archive so that it may be available to future scholars. Leibniz, Wittgenstein, Nietzsche, and Gauss are just a few examples of scholars who left behind extensive Nachlässe. Whitehead chose to eschew this long tradition, and upon his death, "His widow destroyed all of his manuscripts, as he had expressly desired." (ODNB) Whitehead had an almost fanatical belief in the individuals' right to privacy, which explains his wishes to have his papers destroyed; he rarely even wrote letters to friends or colleagues. In 2011, a 6-page letter from Whitehead was donated to the Library of Congress from the estate of Whitehead's former assistant. In honor of this most rare item, the Library of Congress held a symposium focusing "on the historical context of the letter and on Whitehead and his intellectual focus in a number of fields... Whitehead seldom corresponded with anyone, and a receipt of a letter by his friends or colleagues was described as 'rare and cause of a communal celebration'... Further, Whitehead's family carried out his instructions and destroyed his papers." ("Experts to Discuss Famed Mathematician and Philosopher Alfred North Whitehead and a Rare Piece of Correspondence at Symposium on Feb. 17," Library of Congress News).
In the present manuscript, likely written ca 1900, possibly in early preparation for his magnus opus, Principia Mathematica, Whitehead takes a deep look at several issues in mathematics, primarily in regards to bilinear forms, homogeneous functions, and quadratic forms, as discussed in the work of mathematicians Karl Weierstrass and Ferdinand Georg Frobenius, and citing the work of several other mathematicians, most notably George Salmon. Widely known as the “father of modern analysis” Weierstrass was a German mathematician who was one of the founders of the modern theory of functions. Very interested in the soundness of calculus, he made great contributions to the theories of periodic, elliptic, and Abelian functions, functions of real variables, the calculus of variations, and as in the second work analyzed in the present manuscript, bilinear and quadratic forms.
The first section, titled "Weierstrass Monatsberichte der Königl. Akad. zu Berlin. 1858" and subtitled "Über ein die homogenen Functionen zweiter Grades betreffen des Theorem" consists of an analysis and partial translation into English of Weierstrass' 1858 paper on homogenous functions and bilinear forms. Here, Whitehead translates the equations set forth in Weierstrass’ paper, showing their proofs, often noting limitations or lack of clarity to the notation, and expanding upon them. Whitehead references the work of several other prominent mathematicians, applying their work to Weierstrass’ equations. For example, on f 7, Whitehead applies the theory of determinants set forth in George Salmon’s 1876 work Lessons Introductory to the Modern Higher Algebra, to Weierstrass’ equations (14)-(17) as follows: “Now from the theory of determinants (of Salm. High. Alg. §33) = si= the product of and an integr[al] function of s. Thus ? (14) Also ? (15) Hence from (14) and (15) is =, where is a linear function of , , ... Thus if ++... + ? (16)
? (17)” Whitehead often expands and improves upon Weierstrass’ work, notably for proofs 24 & 25, for which Whitehead gives his own lengthy proofs, including a 3 page proof for (24) beginning:
“To prove that ?? is a (?-1) fold root of ??(s)=0,” and another 3 page proof beginning “Now the roots of (1)=0 are all real: this follows from the proof when the roots are all different... Hence (3)?? is divisible by (s-sµ)l-1. QED.”
Whitehead also makes alterations or improvements to Weierstrass’ notation, such as on ff 42v “Note Weierstrass’ notation is slightly altered here” or simply points out problems with the notations, such as on ff 46v “These are the forms of Eq |38| given by Weierstrass; but his notation is not explained very clearly.”
The second section, titled "Weierstrass. Berliner Berichte 1868. Zu theorie der bilinearen und quadratischen Formen" is the lengthiest. It consists of an analysis and partial translation into English of Weierstrass' 1868 paper on bilinear and quadratic forms. Similar to what he did in the first section, Whitehead here analyzes the equations set forth in Weierstrass’ above mentioned paper, again adding, expanding, and noting limitations or problems with Weierstrass’ work. For example, Whitehead takes a close look at Equations 38-48, comparing equations 40 and 34 with 38 “Hence by comparison with (40) and (34)... It has been assumed that P and Q are such that the highest power of each linear element of S which occurs is the G.C.M...” and showing that equations 43-48 still hold. Whitehead then points out on ff 5 of notebook 2 “The proof of this assumption has been given much better by Frobenius in Berliner Sitzungberichte, 1894, and the proof originally given is now omitted.”
The third section consists of an analysis and partial translation into English of Frobenius' proof of Weierstrass' theorem, as given in Frobenius’ 1894 paper “Über die Elementartheiler der Determinanten.” Frobenius was a German mathematician most known for his contributions to the theory of elliptic functions, differential equations, and to group theory. Frobenius was a student of Weierstrass and was supervised by him in 1870 at the University of Berlin. He was later appointed to a teaching position at the University which "...must ultimately have been made possible due to strong support from Weierstrass who was extremely influential, and considered Frobenius one of his most gifted students." (O'Connor & Robertson) Whitehead compares Frobenius’ proof to that of Weierstrass’ writing “Frobenius’ Proof of Weierstrass’ Theorem that a set of minors of S can be found of the... This is equivalent to the theorem assumed by Weierstrass of Frobenius in “Über die Elementhartheiler der Determinanten – Sitzungberichte der Akad. Zu Berlin. 1894.”
Whitehead is best known for his early mathematical work, most notably the Principia Mathematica (1910-1913), a three-volume work which he wrote with his former student Bertrand Russell. It is now considered to be one of the most important 20th century works of mathematical logic. In their research for the work ""They arrived at the 'logicist' position, that mathematics is a part of logic, so that a separate philosophy of mathematics does not exist, a view contradicting the Kantian doctrine that mathematical proofs depend on a priori forms of intuition. The investigation was published in the three colossal volumes of Principia Mathematica which appeared in 1910-13, and which formed the greatest single contribution to symbolic logic for the time." (ODNB) Weierstrass was a great influence on Whitehead and Russell in their formation of theories about logicism. Written as a defense of logicism, the view that some or all of mathematics can be reduced to formal logic, the Principia Mathematica was instrumental in developing and popularizing modern mathematical logic. "The logicist thesis appears to have been first advocated in the late seventeenth century by Gottfried Liebniz. Later, the idea was defended in much greater detail by Gottlobe Frege. During the critical movement of the 1820s, mathematicians such as Bernardo Bolzano, Niels Abel, Louis Cauchy, and Karl Weierstrass succeeded in eliminating much of the vagueness and many of the contradictions present in the mathematics of their day." (Stanford Encyclopedia of Philosophy) In the late 1910s-20s, Whitehead shifted his focus to the philosophy of science and metaphysics, and to the concept of eliminating the infinitesimal. Whitehead continued to be influenced by the work of Weierstrass during this period, who was also known for his work on the concept of eliminating the infinitesimal, and as Bertrand Russell points out in his Introduction to Mathematical Philosophy (1919) "It has been thought ever since the time of Leibniz that the differential and integral calculus required infinitesimal quantities. Mathematicians (especially Weierstrass) proved that this is an error; but errors incorporated, e.g. in what Hegel has to say about mathematics die hard, and philosophers have tended to ignore the work of such men as Weierstrass. Limits and continuity of functions in works on ordinary mathematics are defined in terms involving numbers. This is not essential as Dr. Whitehead has shown."
Weierstrass’ influence is found in nearly all of Whiteheads' work, including in 1929 Process and Reality. An Essay in Cosmology. "The speculative philosophy that Alfred North Whitehead developed in Process and Reality is profoundly influenced by a mathematical assumption - namely, that 'there are no infinitesimals.'" (Lango, John Whitehead's Actual Occasions and the New Infinitesimals) In Process and Reality, in reference to measurement as a comparison of infinitesimals and the theory of extension, Whitehead writes "The answer to this problem is that there are no infinitesimals, and that therefore there can be no approximation to them. In mathematics, all phraseology about infinitesimals is merely disguised statement about a class of finites. This doctrine has been conclusive mathematical theory since the time of Weierstrass in the middle of the nineteenth century."
Process and Reality is considered "Whitehead's most comprehensive (but difficult to penetrate) metaphysical work. Together, his three books The Concept of Nature (1920), Science and the Modern World (1925), and Process and Reality (1929) provide a relatively complete statement of Whitehead's mature metaphysical system." (Stanford Encyclopedia of Philosophy)
Literature: Dictionary of Scientific Biography, pp 302-308; Frobenius, Ferdinand Georg "Über die Elementartheiler der Determinanten." In: Sitzungberichte der Königsliche Presussischen Akademie der Wissenschaften zu Berlin, 1894, pp 31-44; Frobenius, Ferdinand Georg "Über das Trägheitsgesetz der quadratischen Formen." In: Sitzungberichte der Königsliche Presussischen Akademie der Wissenschaften zu Berlin, 1894, pp 407-431; Henry, Granville C. & Robert J. Valenza "Whitehead's Early Philosophy of Mathematics." In: Process Studies, Vol. 22, Number 1, Spring, 1993, pp 21-36; O'Connor & Robertson, Ferdinand George Frobenius, http://www-history.mcs.st-andrews.ac.uk/Biographies/Frobenius.html; Oxford Dictionary of National Biography; Russell, Bertrand Introduction to Mathematical Philosophy. London: George Allen & Unwin, 1920; Salmon, George Lessons Introductory to the Modern Higher Algebra. Dublin: Hodges, Smith & Co, 1859; Weierstrass, Karl "Über ein die homogonen Functionen zweiten Grades betreffendes theorem, nebst Anwendung desselben auf die theorie der kleinen Schwingengen." In: Monastberichte der Akademie der Wissenchaften zu Berlin, 1858, pp 207-220; Weierstrass, Karl "Zur theorie der bilinearen und quadratischen Formen." In: Monastberichte der Akademie der Wissenchaften zu Berlin, 1856, pp 310-338; Whitehead, Alfred North An Introduction to Mathematics. New York: H. Holt and Company, (1911).
Provenance: Ex library of Alfred North Whitehead, found tied together with his daughter Jessie M. Whitehead's notebook. Full description and research by Cassandra Hatton
HBS 67726
$125,000 .
Price: $125,000.00
Item #67728